|
|
| Un mètre cosmique |
Comment mesurer la courbure de
l'Univers ?
|
| Une réponse toute simple à cette
question est : «
Trouvez une bonne règle étalon et l'utiliser !
» Tout ce qu'il faut, c'est trouver le bon mètre, qui soit valable aux
distances cosmiques.
Tout d'abord, entendons-nous sur la notion de
courbure. Si l'Univers est courbe,
par exemple comme la surface de la Terre qui est presque sphérique,
alors la relation entre la distance d'un objet et son angle ne sera
pas ce que l'on attend dans le cas d'un espace plat.
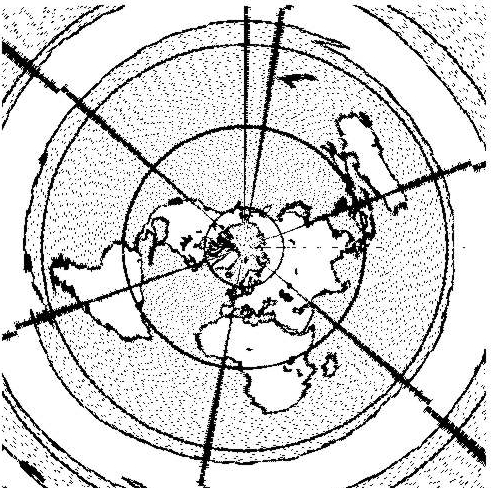
Si quelqu'un, au pôle Nord, dessine, sur une feuille de papier, une
carte du monde, en se plaçant lui-même au centre, il trouvera que
l'Antarctique est un continent énorme en forme d'anneau, et que les
dimensions des pays du Sud sont exagérées par rapport à leurs étendues
réelles. S'il connaît les tailles réelles de tous ces pays lointains,
notre géographe du Nord pourrait en déduire que la surface de la
planète n'est pas plane, mais sphérique.
|
|
 |
Les astronomes tentent le même exercice en trois dimensions. Si on
connaît par avance les tailles réelles des objets lointains, et si
leurs tailles angulaires mesurées s'avèrent plus grandes, égales, ou
plus petites que celles prévues par la géométrie plane, on peut en
déduire que l'espace est sphérique, plat ou encore hyperbolique, un
peu comme une surface en forme de selle de cheval.
La courbure de l'Univers est fonction de deux paramètres de
l'Univers : d'une part, le paramètre de
densité, qui vaut 1 si
la densité de l'Univers est juste assez grande pour que son expansion
ralentisse sans cesse, presqu'au point de s'arrêter, et d'autre part,
la constante cosmologique,
représentant une énergie additionnelle de l'Univers, dont la nature
reste encore mystérieuse, et qui contribue à accélérer l'expansion de
l'Univers. La théorie des tous premiers instants de l'Univers suggère
que l'Univers puisse être presque plat,
ce qui implique que la somme de ces deux paramètres doit
valoir à peu près 1.
|
|
|
|
Pour mesurer la courbure, il faut donc disposer d'objets lointains
de dimension connue et qui peuvent servir de
règles étalons cosmiques. |
Deux chercheurs,
Boud Roukema,
à l'IUCAA, en
Inde (et visiteur au DARC,
Observatoire de Paris-Meudon) et
Gary Mamon, à l'IAP (et
associé au DAEC,
Observatoire de Paris- Meudon), ont proposé d'employer la taille
moyenne des « bulles » des grandes
structures de l'Univers, tracées par des galaxies, comme étalon
statistique pour mesurer la courbure
de l'Univers.
En effet, aux très grandes échelles de l'ordre de plusieurs
centaines de millions d'années-lumière, la gravitation n'influence que
très faiblement les mouvements relatifs (même si elle est d'une
importance primaire dans l'expansion moyenne de l'Univers). Ainsi,
dans une carte compensée de cette expansion, les très grandes
structures devraient rester à peu près figées dans le temps (mais
deviendraient plus marquées, par attraction de la matière
environnante). En un mot, elles servent d'étalon dans un repère dit
comobile avec l'expansion de
l'Univers. |
Dans l'Univers local, représentant les conditions de l'Univers au
temps présent, de telles structures de
galaxies sont bien connues depuis la découverte du Grand
Mur par Valérie de
Lapparent (IAP) et ses collègues au milieu des années 80.
Il suffirait de détecter ces structures à grande distance à l'aide
d'objets assez brillants et ensuite de rechercher les valeurs que
doivent avoir les paramètres de courbure afin que les bulles
lointaines aient, en moyenne, la même taille que les bulles locales.
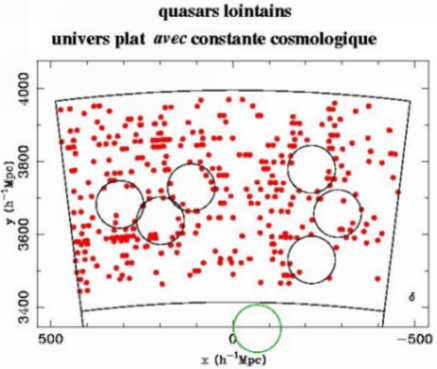
L'image ci-dessous montre que les deux chercheurs ont trouvé des
bulles parmi les quasars
lointains. Mais pour que ces bulles aient la même taille (les figures
sont corrigées pour l'expansion de l'Univers) que les bulles de
l'Univers local, il faut que le paramètre de
densité vaille environ 0,3, tandis que la constante
cosmologique n'est que très faiblement contrainte. Ainsi, cette
approche de la géométrie de l'Univers produit la même valeur du
paramètre de densité que l'étude des mouvements des galaxies dans les
amas et dans les groupes de galaxies. |
 |
Si
on combine cette analyse avec celles d'autres équipes qui utilisent
des supernovae (étoiles qui explosent) dans les galaxies lointaines,
et qui en déduisent que la constante cosmologique est non-nulle, on
arrive à la conclusion que l'Univers est
presque plat et que le modèle de l'Univers en accélération
(avec constante cosmologique non-nulle) semble être le bon. |

Les cercles dessinés sur l'image de l'Univers proche (centre du
diagramme, sondage
Las Campanas) montrent
d'une façon simple la distribution spatiale des galaxies, en forme de
bulles et de vides, de taille similaire à celle du Grand Mur.
|
|
Si le modèle plat avec
constante cosmologique est le bon, alors des cercles de la même taille
devront pouvoir être dessinés sur l'image du
haut (points en rouge, où le modèle de courbure est celui
avec paramètre de densité égal à 0,3 et
constante cosmologique égale à 0,7) pour tracer les grandes
structures distantes. C'est bien le cas.
|
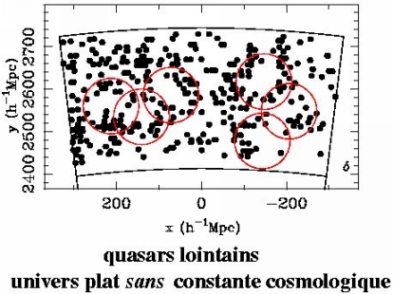
Si le modèle (encore très à la mode
récemment) de l'univers plat sans
constante cosmologique était le bon, alors on pourrait copier les cercles du
sondage proche sur les structures du sondage des
quasars lointains montré en bas (points en noir, pour
paramètre de densité égal à 1 et sans constante
cosmologique). Or, les cercles sont trop grands, ou plutôt, les
bulles des grandes structures ne sont pas suffisamment grandes.
|
|
Il est clair que, c'est la carte du haut,
et non celle du bas, qui donne le bon choix des paramètres de courbure :
l'Univers est presque plat avec une constante
cosmologique non-nulle ! |
Dans un proche avenir, les équipes françaises
espèrent détecter le même genre de distribution des galaxies, des quasars et
du gaz chaud à grande distance, dans les nouveaux grands relevés, par
exemple dans le relevé profond
VIRMOS, qui est en cours actuellement sur le grand télescope européen,
le
VLT. Avec ces données, nous en déduirons des contraintes sur la courbure
de l'Univers et sur la constante cosmologique encore plus précises que
celles que nous venons d'obtenir. |
|
|