LA DÉTECTION DU RAYONNEMENT GRAVITATIONNEL

Le 14 septembre 2015, les détecteurs d'ondes gravitationnelles de la collaboration LIGO/VIRGO ont observé le signal de la coalescence de deux trous noirs ayant des masses de 36 et 29 masses solaires à une distance d’environ 1,3 milliards d'années-lumière. Cette découverte extraordinaire ouvre la voie à l'astronomie des ondes gravitationnelles. D'énormes avancées tant en astrophysique qu'en physique fondamentale sont attendues dans les prochaines années. Des chercheurs de l'Institut d’astrophysique de Paris ont été pionniers dans le développement de nouvelles méthodes permettant d'obtenir, à partir de la théorie de la relativité générale, une prédiction très précise pour la forme d'onde du signal gravitationnel attendu lors de la coalescence d'étoiles à neutrons ou de trous noirs. Ces méthodes sont fondées sur des approximations analytiques en relativité générale, et notamment sur le développement dit « post-newtonien ». Les gabarits d'ondes gravitationnelles post-newtoniens jouent un rôle crucial dans le processus de détection et d'analyse du signal dans les détecteurs d'ondes gravitationnelles. La forme d'onde post-newtonienne est valable dans la phase initiale spiralante de la coalescence et se raccorde aux calculs numériques pour la fusion finale des deux trous noirs.

Une découverte majeure

Les ondes gravitationnelles sont des vibrations de l'espace-temps prédites par la théorie de la relativité générale (Figure 1). Elles se propagent à la vitesse de la lumière et sont engendrées par le déplacement très rapide (dit « relativiste ») de quantités importantes de matière.

Les propriétés des ondes gravitationnelles sont très différentes de celles des ondes électromagnétiques. Produites par le mouvement d'ensemble de grandes masses (au contraire de la lumière qui est généralement engendrée par la superposition incohérente des émissions des atomes individuels qui composent la source), on peut les considérer comme une sorte d'analogue des ondes sonores. De plus les ondes gravitationnelles interagissent extrêmement faiblement avec la matière, et peuvent donc se propager sans être affectées sur des très grandes distances. L'astronomie des ondes gravitationnelles, qui démarre avec cette découverte, sera donc complémentaire de l'astronomie traditionnelle qui explore le rayonnement électromagnétique (dans toutes les gammes de longueur d'onde, radio, visible, X, etc.). Elle permettra d'étudier des évènements violents souvent invisibles en rayonnement électromagnétique et survenant à très grandes distances dans l'Univers.

Le 14 septembre 2015, à 9 heures 50 minutes et 45 secondes exactement en temps universel, le détecteur LIGO (Laser Interferometric Gravitational Observatory) situé sur la côte est américaine dans l'état de Louisiane, observa le signal d'une onde gravitationnelle qui avait été émise lors des derniers instants d'un système de deux trous noirs^[1], au moment où les deux trous noirs sont entrés en collision et ont fusionné. Cet événement a été baptisé « GW150914 » (GW pour « gravitational wave », suivi de la date) et s'est produit il y a environ 1,3 milliards d'années. Depuis, l'onde gravitationnelle a voyagé jusqu'au nous, où elle a provoqué sur Terre une infime vibration de l'espace-temps. Cette vibration s'est traduite par une déformation du détecteur, qui a été mesurée grâce à une technique très poussée d'interférométrie à laser (une méthode de mesure par interférence entre deux faisceaux laser, qui permet de mesurer les variations de distance avec une extrême précision). Le détecteur lui-même est un interféromètre géant avec des bras de 4 kilomètres de long. Le même signal a été observé quelques millisecondes après par l'autre détecteur LIGO situé sur la côte ouest américaine, dans l'état de Washington. La différence entre les temps d'arrivée du signal dans les deux détecteurs a permis d'avoir une information sur la direction dans le ciel dans laquelle s'était produit l'évènement.

Les images des signaux ont tout d'abord été obtenues immédiatement à l’arrivée de l’onde dans un diagramme dit de « temps-fréquence » qui permet de caractériser rapidement les événements intéressants par leur montée en fréquence au cours du temps (Figure 2). L'amplitude de l'onde gravitationnelle, qui caractérise la déformation de l'espace-temps engendrant les vibrations du détecteur, a ensuite été directement mesurée (Figure 3). Lors de la détection en ligne, c’est-à-dire effectuée simultanément aux mesures de l’instrument, les algorithmes d'analyse du signal déterminèrent que la combinaison des deux masses qui paramétrise l'onde en première approximation est trop importante pour que le signal soit dû à des étoiles à neutrons^[2]. On a donc affaire à une paire de trous noirs en train de fusionner, qui est illustrée par une simulation numérique dans la Figure 4. Les masses des deux trous noirs les plus probables, déterminées lors d'une analyse plus fine faite après la détection en ligne, sont de 36 et 29 fois la masse du Soleil (Figure 5). Ces valeurs sont nettement plus grandes que les masses des trous noirs connus dans notre Galaxie et d'origine stellaire, c'est-à-dire produits par l'explosion d'étoiles appelées supernovae. Ce résultat pose un défi aux modèles d'évolution stellaire actuels et soulève la question de la population d'étoiles très massives qui aurait pu conduire à la formation de tels trous noirs.

La distance de la région de l’Univers dans laquelle s'est produite cette coalescence est de 1,3 milliards d'années-lumière (soit environ 400 megaparsec), ce qui correspond à un décalage vers le rouge d’environ 0,1 (observé par une récession cosmologique des galaxies dans l’Univers en expansion de l’ordre de un dixième de la vitesse de la lumière). Entre la Terre et cette distance se trouvent de nombreuses galaxies. Néanmoins, cette distance est relativement proche par rapport aux très grandes distances (dites « distances cosmologiques ») que les futurs observations d'ondes gravitationnelles exploreront.

La distance se mesure directement avec l'amplitude de l'onde gravitationnelle et l’augmentation de la fréquence du signal durant l’évènement. L'amplitude gravitationnelle à la distance de 400 megaparsecs est de l'ordre de 10^-21, ce qui représente exactement la variation minuscule de longueur relative des bras de 4 km de long du détecteur causée par le passage de l'onde gravitationnelle. Le rapport entre le signal détecté et le bruit du détecteur, somme de tous les bruits causés par l'instrument et son environnement terrestre, est important, de l'ordre de 25. La probabilité que ce signal soit dû à une fluctuation statistique du bruit (ce qu'on appelle la probabilité de fausse alarme) est de l'ordre de un sur 10 millions (soit 10^-7, ce qui correspond, dans le jargon statistique, à une détection à 5 « sigma gaussien »). La détection est donc robuste et sans équivoque !

Au moment où les deux trous noirs ont été détectés, c'est-à-dire lorsque la fréquence du signal gravitationnel est entrée dans la bande de fréquence des détecteurs à environ 35 Hz (Figure 2), ils étaient distants l’un de l’autre d'environ 1000 km. Le rayon de chacun des trous noirs est de l'ordre de 100 km. Pendant la fraction de seconde qu’a duré l’évènement (un cinquième de seconde), ceux-ci ont parcouru une dizaine de cycles orbitaux sur une trajectoire en spirale selon laquelle les deux corps se rapprochent, à cause de la perte d'énergie due à l'émission des ondes gravitationnelles. Juste avant la coalescence, la vitesse de déplacement des trous noirs sur cette orbite atteignait la moitié de la vitesse de la lumière ! La fréquence du signal au moment de la coalescence est de 150 Hz (Figure 2), ce qui est proche du maximum de sensibilité des détecteurs. Les deux trous noirs formèrent finalement un trou noir massif unique, tout d'abord fortement déformé à cause de la collision, puis qui s'est « relaxé », c’est-à-dire a atteint un état stationnaire par dissipation d’énergie, toujours en émettant des ondes gravitationnelles. Cette émission s'est faite dans les modes dits « quasi-normaux », qui sont caractéristiques des modes de résonance du trou noir. Après l'émission de tous ses modes quasi-normaux, le trou noir devient ce qu'on appelle un « trou noir de Kerr », décrit seulement par sa masse et sa rotation (ou « spin ») dans le contexte de la théorie de la relativité générale. Dans le cas de GW150914, la masse du trou noir final est de 62 masses solaires et son spin, c’est-à-dire son moment cinétique lié à la vitesse de rotation de la surface du trou noir, est estimé à 0,7 en unité de la vitesse de la lumière (le spin maximal possible étant un).

La différence entre la somme des masses des deux trous noirs initiaux et la masse du trou noir final est d'environ 3 fois la masse du Soleil. Qu'est devenue cette masse ? Elle a été convertie en énergie purement gravitationnelle et emportée en une fraction de seconde par l'onde gravitationnelle ! On évalue donc la puissance émise par cet évènement sous forme d'ondes gravitationnelles à 10⁵⁵ erg par seconde, soit l’équivalent de l'énergie totale d’environ 1000 explosions de supernovae émise en une fraction de seconde, une valeur colossale.

La contribution de la théorie à cette découverte

Grâce à un fort rapport signal-sur-bruit et une fréquence maximale dans la meilleure plage de sensibilité des détecteurs, cet évènement extraordinaire donne accès aux trois phases successives de la coalescence, la phase initiale spiralante avec une dizaine de cycles orbitaux, la phase de fusion très courte et enfin la phase de relaxation du trou noir final (Figure 6). L'analyse du signal dans les trois phases montre que celui-ci est en accord avec les prédictions de la relativité générale. Aucune déviation par rapport à cette théorie n'est mise en évidence.

La cohérence entre le signal observé et celui attendu par la théorie est évidemment un aspect extrêmement important du processus de détection. En effet, une telle découverte ne peut se faire que si l'on est convaincu que le signal correspond à un phénomène physique réel prévu par la théorie et décrit avec précision. Sans la théorie, aucune détection n'est possible, car un signal non modélisé (pour lequel on n'a aucune interprétation physique) peut être vu comme une fluctuation statistique du bruit dans le détecteur.

Le grand intérêt des systèmes binaires^[3] d'objets compacts (qui sont soit des étoiles à neutrons, soit des trous noirs), est que l'onde gravitationnelle qu'ils émettent est calculable avec grande précision en relativité générale. On peut montrer que les effets non gravitationnels, qui sont très importants dans le cas des systèmes d'étoiles normales (comme la présence d'un disque d'accrétion de matière autour des étoiles, ou les effets du milieu interstellaire et des champs magnétiques, ou même de la structure interne de la matière dense dans les étoiles à neutrons), ont un impact négligeable sur la dynamique et le rayonnement des objets compacts. Le problème à résoudre est donc essentiellement celui du problème à deux corps en relativité générale.

Dans la phase initiale spiralante, les objets compacts sont assez éloignés l'un de l'autre, leur vitesse orbitale est faible par rapport à la vitesse de la lumière, et le système peut être modélisé par deux masses ponctuelles. L'onde gravitationnelle est alors calculée grâce à l'approximation dite « post-newtonienne », qui est un développement de la relativité générale lorsque la vitesse des corps est petite par rapport à la vitesse de la lumière. Dans cette limite, la relativité générale se ramène à la théorie de Newton. L'approximation post-newtonienne a été à la base de quasiment tous les succès de la relativité générale quand il s'agissait de comparer ses prédictions avec les observations (avance du périhélie de l'orbite de Mercure, déviation de la lumière par le Soleil, etc.). Dans le cas des ondes gravitationnelles émises par les binaires compactes spiralantes, l'approximation post-newtonienne consiste à développer le signal au-delà de la formule du quadrupôle d'Einstein (Figure 1). Il s'est avéré nécessaire de développer cette approximation jusqu'à un très haut niveau de précision.

Les physicien-ne-s de l'IAP et leurs collaborateurs ont mis en place à partir des années 1990, un formalisme nouveau pour le calcul de l'onde gravitationnelle émise par un système de matière en relativité générale, et ont ensuite appliqué ce formalisme au cas des systèmes binaires d'objets compacts spiralants. La prédiction post-newtonienne issue de ces calculs est donnée par des formules mathématiques qui sont maintenant utilisées par tous les détecteurs d'ondes gravitationnelles pour rechercher et analyser le signal des systèmes binaires coalescents dans leur phase spiralante.

La méthode post-newtonienne n'est plus valable lorsque les deux trous noirs entrent en contact et fusionnent. Pour la phase de fusion la prédiction théorique de la relativité générale doit être obtenue par d'énormes calculs numériques sur ordinateur. Pendant longtemps, les calculs numériques ont constitué un véritable défi pour les physicien-ne-s, mais ils ont finalement abouti en 2005. En revanche, ces calculs numériques sont inadaptés dans la phase spiralante à cause de temps de calcul extrêmement long. Les physicien-ne-s disposent donc maintenant de la solution numérique « exacte » pour la phase de fusion, ainsi que pour la phase de relaxation. La solution numérique se raccorde avec une grande précision à la solution post-newtonienne décrivant la phase spiralante (Figure 6). D'autres méthodes analytiques ont aussi été développées, qui reviennent à remplacer le problème physique réel à deux corps (grâce à des techniques de « resommation » de la série post-newtonienne) par un problème plus simple dit « effectif à un corps » (« effective one body », ou « EOB »). Cette approche a été confirmée et améliorée par les calculs numériques sur ordinateur. L'analyse des données des expériences comme celle de la collaboration LIGO/VIRGO exploite ce type de solution effective, qui est très utile en pratique car elle permet d'explorer en temps réel, c’est-à-dire au moment de la détection, une grande région de l’espace des paramètres (notamment les masses des trous noirs).

C'est donc grâce à la combinaison de la méthode analytique d'approximation post-newtonienne, extrêmement précise pour les grandes séparations orbitales mais cessant d'être valable au moment de la fusion, et de calculs numériques exacts dans les phases de fusion et de relaxation, qu'est résolu le problème de la coalescence de deux objets compacts en relativité générale. C'est la solution de ce problème qui est utilisée pour la recherche et l'analyse du signal des ondes gravitationnelles.

Dans le cas de trous noirs massifs comme pour GW150914, la plus grande partie de la détection intervient lors de la phase de fusion des trous noirs et la prédiction numérique joue donc le rôle le plus important. On n'observe en effet qu'une dizaine de cycles orbitaux avant la coalescence (Figure 5). Dans le cas de trous noirs moins massifs, ou alors de systèmes binaires d'étoiles à neutrons (une source d'ondes gravitationnelles que les physicien-ne-s sont certain-e-s d'observer au moins une fois par an avec LIGO, grâce aux décompte des pulsars doubles dans notre galaxie), les détecteurs seront très sensibles lors de la phase spiralante, qui comprendra des milliers de cycles observables, et l'approximation post-newtonienne jouera un rôle déterminant.

Notes

[1] Un trou noir est un objet si compact que l'intensité de son champ gravitationnel empêche toute matière ou rayonnement de s’en échapper. Un tel objet ne peut ni émettre, ni réfléchir la lumière, il est donc en principe noir. Toutefois ceci n'est vrai que dans le cadre classique de la relativité générale: on sait, depuis les travaux de Hawking, qu'un trou noir émet du rayonnement à cause d'effets de physique quantique ; mais ce rayonnement est négligeable pour les trous noirs de grande masse, comme c’est le cas pour GW150914.
[2] Une étoile à neutrons est le résidu d'une étoile massive ayant explosé en supernova, et est composée essentiellement de neutrons maintenus ensemble par la gravitation. Elle est difficilement observable, sauf si elle se manifeste par une émission radio pulsée (on dit alors qu’il s’agit d’un pulsar), ou par la présence d'un disque d'accrétion provenant de l'arrachage de matière à une étoile compagnon.
[3] Un système binaire en astronomie est un ensemble composé de deux objets de l’Univers liés par la force de gravitation, et qui sont donc en orbite autour de leur centre de gravité commun.

Lien

 Article dans Living Review in Relativity : Blanchet, 2014, « Gravitational radiation from post-Newtonian sources and inspiraling compact binaries ».

Rédaction et contacts

• Luc Blanchet
  Institut d’astrophysique de Paris, CNRS, UPMC
  luc [point] blanchet [à] iap [point] fr
  
• Guillaume Faye
  Institut d’astrophysique de Paris, CNRS, UPMC
  guillaume [point] faye [à] iap [point] fr
  

Rédaction web : Valérie de Lapparent
Mise en page : Jean Mouette

Figures

Figure 1

Un an après sa formulation de la théorie de la relativité générale en novembre 1915, Einstein prédisait l'existence des ondes gravitationnelles. Puis, en 1918, il obtenait la célèbre formule dite du « quadrupôle » qui donne l'énergie émise sous forme d'ondes gravitationnelles par un système de matière. La preuve de l'existence des ondes gravitationnelles (et de la validité de la formule du quadrupôle) a été apportée en 1979 grâce aux observations du mouvement du pulsar binaire PSR 1913+16 découvert par Hulse et Taylor (prix Nobel en 1993). Crédits : DR.

Figure 2

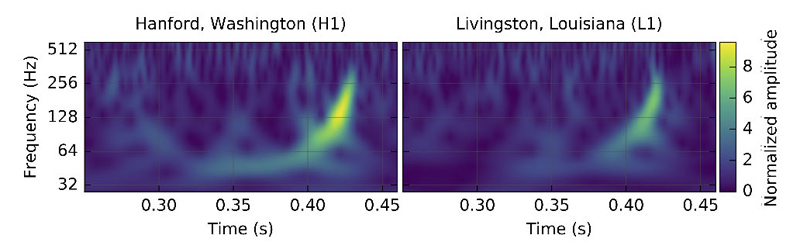
L'onde gravitationnelle observée par les deux détecteurs LIGO de Hanford et Livingstone dans un diagramme donnant l’évolution de la fréquence avec le temps. Pour une onde, la fréquence mesure le nombre d’oscillations par seconde. Dans le cas d'une onde gravitationnelle, la montée en fréquence du signal (en forme de « girafe ») est caractéristique d'une coalescence de deux objets compacts. Crédits : collaboration LIGO/VIRGO.

Figure 3


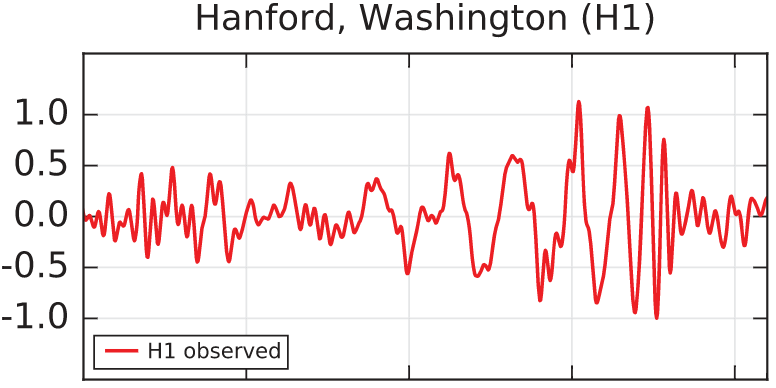
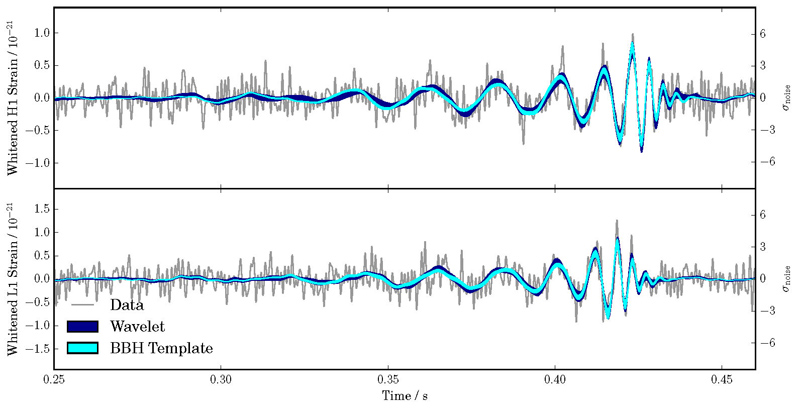
En haut : le signal brut observé par le détecteur LIGO situé à Hanford, en unité de 10^-21 fois la variation relative de longueur des bras de l’interféromètre.
En bas : les deux signaux observés sur les deux sites de Hanford et Livingstone. Les temps d'arrivée des deux signaux sont séparés de 7 millisecondes. En bleu est montré un ajustement des données par une somme d'ondelettes (une description mathématique du signal, mais qui n'est pas physique) et en cyan le meilleur « gabarit » d'onde gravitationnelle qui représente la prédiction physique issue de la relativité générale. Crédits : collaboration LIGO/VIRGO.

Figure 4

Un système binaire de deux trous noirs très proches de la coalescence finale. Le champ gravitationnel intense distord par l'effet de déviation gravitationnelle de la lumière l'image des étoiles situées à l'arrière-plan. Crédits : SXS - Simulating eXtreme Spacetimes.

Figure 5

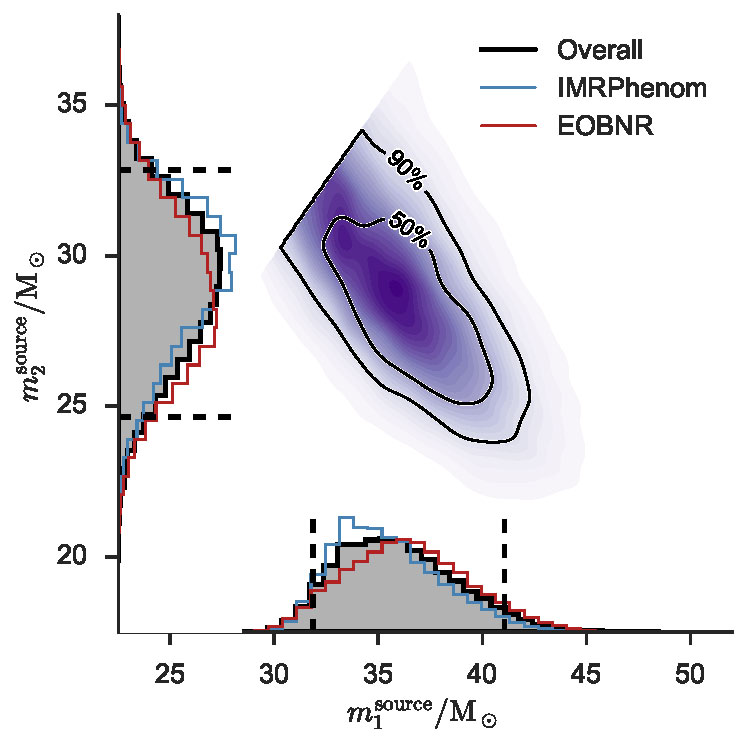
Les masses des trous noirs sont mesurées par comparaison avec des prédictions théoriques combinant les calculs analytiques et numériques en relativité générale. Les courbes de niveaux indiquent la probabilité que l’on ait deux valeurs simultanées des masses m1 et m2 pour les deux trous noirs. Les courbes le long de chaque axe montrent les distributions de probabilité pour la masse de chaque trou noir. Les pics de ces courbes indiquent les deux valeurs les plus probables pour l’évènement GW150914, soit 36 fois la masse du Soleil pour m1, et 29 fois pour m2, avec une incertitude d’environ 4 masses solaires pour chacun. Crédits : collaboration LIGO/VIRGO.

Figure 6

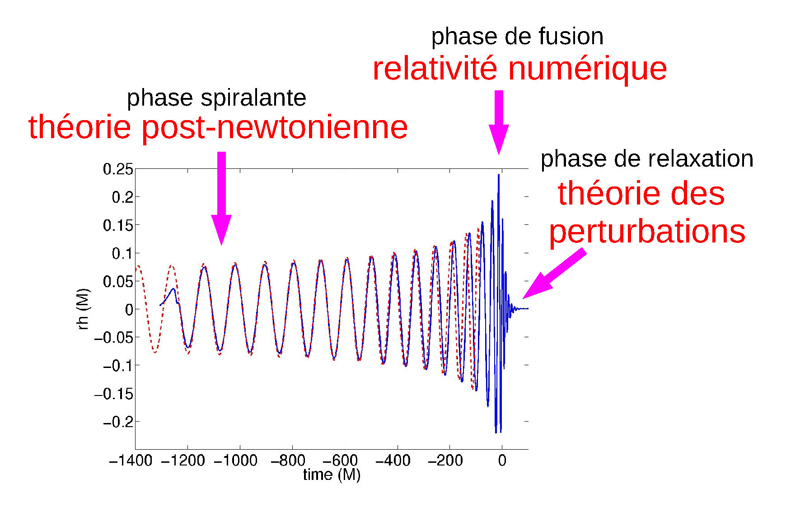
L'onde gravitationnelle dans les trois phases de la coalescence d'un système double d'objets compacts, et les méthodes utilisées pour la déterminer. Le calcul post-newtonien valable dans la phase spiralante est représenté en pointillés rouges. Il se raccorde avec le calcul numérique valable dans les phases de fusion et de relaxation et qui est représenté en trait bleu. Alternativement, le formalisme « effective one body » (EOB) permet de combiner, pour les phases finales, les résultats de la relativité numérique et ceux de la théorie des perturbations, tout en se raccordant au calcul post-newtonien pour la phase initiale.

Mars 2016

Institut d'Astrophysique de Paris - 98 bis boulevard Arago - 75014 Paris